* Die Entfernung der Erde von der Sonne *

Im folgenden möchte ich versuchen - auch für jene die mit Mathe auf Kriegsfuss stehen - das klassische Verfahren zu schildern mit dem man die Entfernung der Erde von der Sonne bestimmen kann. Diese Entfernung nennt man "Astronomische Einheit", abgekürzt AE.

Alles was wir zu gegenwärtigen Zeitpunkt wissen sollten, ist die Grösse der Erde. Um diese herauszufinden gibt es ebenso schöne Verfahren, die ich hier aber nicht behandle. Wir setzen sie einfach als bekannt voraus. Der Radius der Erde beträgt etwa 6357km, der Durchmesser das Doppelte, 12714km.

Wir begeben uns zunächst einmal gedanklich auf die Sonnenoberfläche; wer es ganz genau meint, kann auch sie sich wegdenken, und zum gedachten Sonnenmittelpunkt weiterreisen. Wenn wir an diesem Ort zum Himmel aufblicken werden wir neben zahlreichen Sternen auch unsere Heimatwelt entdecken können. Ein Blick durch das Teleskop dürfte ein kleines blau-weisses Scheibchen offenbaren; die Sterne bleiben dagegen Punkte.
Dieses Scheibchen nimmt eine bestimme Fläche am Firmament ein.

Wir ziehen nun einen grossen Kreis am Firmament, mit unserem Standort, der Sonne, als Mittelpunkt. Der Kreis soll mitten durch das Erdscheibchen hindurch gehen. Tja, dies ist die Erdumlaufbahn, die "Ekliptik". Einmal rund herum im Kreis, das ist ein Winkel von 360 Grad. Ein klitzekleiner Anteil des Kreises wird vom Erdscheibchen verdeckt; dies sind etwa 17,53 Bogensekunden, oder ungefähr der 74tausendste Teil des gesamten Kreises, genauer 1/73930.
Die Hälfte dieses Wertes trägt übrigens den irreführenden Namen "Sonnenparallaxe", der Winkel unter dem der Erdradius in Sonnenabstand beobachtet wird.

Wir wissen jetzt, dass man auf ihrer Umlaufbahn die Erde 73930 mal hintereinander reihen könnte.
Aha! Jetzt ist es ein Leichtes die Länge der Erdumlaufbahn zu berechnen; dies sind einfach 73930 Erddurchmesser, a 12714km (Poldurchmesser), also die unvorstellbare Strecke von 940 Mio km (also bald 1 Milliarde Kilometer).
Jetzt sind wir fast schon am Ende; Man braucht nur noch in die Formel für den Kreisumfang:

Umfang = 2 * PI * Radius

alle bekannten Werte eintragen:

940 Mio km = 2 * 3,1415 * "Entfernung Erde-Sonne"

und nach der "Entfernung Erde-Sonne" auflösen:

Entfernung Erde-Sonne = 940 Mio km / (2 * 3,1415) = 149,6 Millionen km.

Fertig? Nun, wenn wir uns nur auf die Sonne begeben könnten! Von dort aus haben wir nämlich jene 17,588 Bogensekunden des Erdscheibchens "beobachtet". Aber befinden uns AUF der Erde. Wie können wir da je hoffen die Sonnenparallaxe zu messen?

Wenn wir schon an die gute alte Erde gebunden sind, hilft uns wenigstens die Phantasie weiter.
Wir wollen einmal annehmen, ein Stern der auf Nachtseite der Erde werde plötzlich so verflixt hell, dass die Erde einen sichbaren Schatten auf die Sonnenoberfläche werfe. Das wird wohl nie vorkommen, und wenn, dürften wir dies nicht überleben. Aber wir wollen uns das ja nur vorstellen; Sonnencreme mit Lichtschutzfaktor 1000 inklusive:

Ein entfernter Stern werfe den Schatten der Erde auf die Sonne

Wie hilft uns dies weiter?

Lassen wir einmal die unrealistische Annahme mit dem hellen Stern fallen, d.h. wir knipsen ihn aus, aber ersetzen zuvor den Schatten durch einen gleich grossen Sonnenflecken.
Auch brauchen wir 2 Beobachter, einen am Nord- und einen am Südpol unseres Planeten. Diese Beobachter sind nun genauso weit voneinander entfernt wie jene beiden Sonnenflecken. Jeder Beobachter soll nun auf einen gegenüberliegenden Rand des Sonnenflecks blicken, und zwar so, dass sich ihre Blicke kreuzen. Der Kreuzungspunkt liegt genau auf der Mitte der Strecke Erde-Sonne!

Jetzt setzen wir einen Himmelskörper an genau diesen Kreuzungspunkt. Taufen wir ihn der Kürze halber "Idefix". Unsere Beobachter sehen nun Idefix, und dahinter, sofern er sie nicht vollständig verdeckt, auch noch einen Teil des Sonnenflecken.

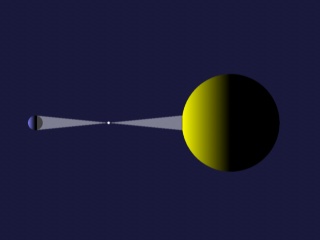Ein Himmelskörper auf halbem Wege zur Sonne bildet den "Erdschatten" in Erdgröße ab

Leider gibt keinen solchen Himmelskörper der exakt den halben Weg markiert. Jedoch gibt es mindestens zwei andere Himmelskörper die nicht genau auf der Hälfte liegen:
Merkur liegt näher an der Sonne als die halbe Erdentfernung (bei 0,38 AE), und Venus liegt weiter entfernt (bei 0,72 AE)

Was geschieht nun, wenn wir Idefix aus seiner Mittellage heraus auf die Sonne zubewegen, also quasi in Richtung Merkur?

Ein ferner Himmelskörper (Merkur) bildet den "Erdschatten" zu klein ab

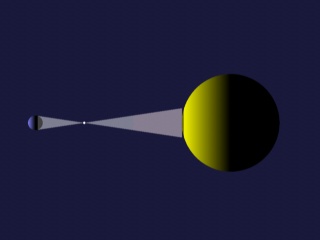Ein naher Himmelskörper (Venus) bildet den "Erdschatten" zu gross ab

Wenn wir nun Idefix durch die Venus ersetzen, messen wir einen Abstand von 45,91 Bogensekunden.

Wir müssten ein Verfahren haben, um aus diesem zu grossen "Venus"-Winkel den richtigen "Erd"-Winkel von 17,59 Bogensekunden zu ermitteln. Offensichtlich hängt dieser Winkel in irgend einer Weise von der Stellung der Venus zwischen Erde und Sonne ab.

Die Venus liegt 0,723 Astronomische Einheiten von der Sonne entfernt. Die Erde, die eine Entfernung von 1 AE von der Sonne hat, ist also 1,0 - 0,723 = 0,277 AE von der Venus entfernt (wenn die Venus in Unterer Konjunktion, das heisst auf einer Linie mit Erde und Sonne steht).

Jetzt kommt der Trick:

Enfernung Erde-Venus / Entfernung Venus-Sonne = 0,277 AE / 0,723 AE = 0,383.
0,383*45,91 Bogensekunden = 17,59 Bogensekunden. Na also!
Der auf der Sonne abgemessene zu grosse oder zu kleine Winkel, ist einfach um das Verhältnis der Streckenlängen Erde-Planet/Planet-Sonne zu korrigieren, und schon ergibt sich der Winkel den wir auf der Sonne ablesen könnten, wenn der entsprechende Körper genau auf halbem Weg zur Sonne läge.

Dieses Verfahren der Verhältnisrechnung ist allerdings nur dann einigermassen genau, wenn wir mit kleinen Winkeln hantierten - aber das ist im Bogensekundenbereich ja der Fall.

Zur Kontrolle und Übung machen wir die Probe mit Merkur, eine Messung ergibt 11,1 Bogensekunden.
Merkur liegt 0,387 AE von der Sonne, und damit 0,613 AE von der Erde entfernt. Wir teilen: 0,613 / 0,387 = 1,584. 1,584 * 11,105 = 17,59 Bogensekunden. Wir sehen uns bestätigt.
(Achtung! Dieses Beispiel mit Merkur ist "hinkt", denn in Wahrheit beschreibt dieser eine Ellipse deren sonnenfernsten Punkt wir hier betrachten.)

Noch einmal das Venusbeispiel, grafisch illustriert:

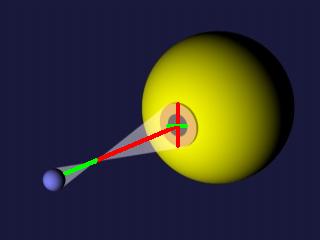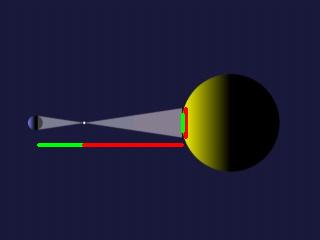Erde-Venus (Grün) / Venus-Sonne (Rot) = 0,383. 0,383 * gemessener Winkel (rot) = Winkelmass des Erddurchmessers. (grün)

Das Quadrat der Umlaufdauer ist proportional zur dritten Potenz des Abstandes zur Sonne. Umlaufdauer² = k * Abstand³, wobei k einfach ein Umrechnungsfaktor ist.

Für die Erde setzen wir nun einfach ein:
Umlaufdauer: 1 Jahr, Abstand 1 AE,
Also (1 Jahr)² = k * (1 AE)³. Aha! jetzt müssen wir den Betrag von k recht einfach wählen nämlich k=1. Dann heisst die ganze "Formel": 1 = 1 * 1, was zweifellos korrekt ist. (Wenn wir mit Tagen oder Kilometern hantiert hätten, wären wir gezwungen einen anderen k-Wert zu wählen)

Was wissen wir von der Venus? Durch Beobachtung wissen wir: Die Venus braucht für einen Sonnenumlauf 0,615 Jahre,
Also 0,615² = 1 * (Venusabstand in AE)³. Die Dritte Wurzel aus 0,615² ergibt den Venusabstand von 0,723 AE.

Was zuletzt noch zu fragen bleibt: Was ist aus Idefix geworden?
Wir brauchen ihn eigentlich nicht mehr; wahrscheinlich ist er auf die Venus gestürzt. Ersatzweise dürfte es aber heuer ausreichend viele Hobbyastronomen geben, die stattdessen die Abstände zweier zeitgleich aufgenommener Venuscheibchen messen.

Und noch ein Nachtrag:
Etwas unsanft habe ich unsere beiden Beobachter vorhin auf Nord und Südpol verbannt. Dies stimmt natürlich so nicht; genaugenommen müssten sie zum Zeitpunkt ihrer Aufnahmen exakt an der Dämmerungsgrenze auf gegenüberliegenden Punkten der Erde stehen, um einen Erddurchmesser Abstand voneinander zu haben. Dies ist natürlich auch unrealistisch; nicht nur wegen der Verfälschungen ihrer Beobachtungen durch die Erdatmosphäre.
Es reicht, die beiden in praktischem, aber bekannten Abstand voneinander aufzustellen, an beliebigen - der Sonne zugewandten - Punkten auf der Erdoberfläche.
Entsprechend kleiner wird der gemessene Winkel sein, und entsprechend kleiner wird die korrigierte Parallaxe ausfallen - aber entsprechend mehr Abschnitte dieser Teilerden sind aneinanderzureihen um den Umfang der Erdbahn zu errechnen, und damit den nach dem Erdumfang zweiten grossen Schritt auf der kosmischen Entfernungsleiter, den Abstand der Erde von der Sonne.